|
|
 |
Archiwum zadań
tygodnia 2020-2021
 |
| |
|
|
 Zadania tygodnia - 2003/2004
Zadania tygodnia - 2003/2004
 Zadania tygodnia - 2004/2005
Zadania tygodnia - 2004/2005
 Zadania tygodnia - 2005/2006
Zadania tygodnia - 2005/2006
 Zadania tygodnia - 2006/2007
Zadania tygodnia - 2006/2007
 Zadania tygodnia - 2007/2008
Zadania tygodnia - 2007/2008
 Zadania tygodnia - 2008/2009
Zadania tygodnia - 2008/2009
 Zadania tygodnia - 2009/2010
Zadania tygodnia - 2009/2010
 Zadania tygodnia - 2010/2011
Zadania tygodnia - 2010/2011
 Zadania tygodnia - 2011/2012
Zadania tygodnia - 2011/2012
 Zadania tygodnia - 2012/2013
Zadania tygodnia - 2012/2013
 Zadania tygodnia - 2013/2014
Zadania tygodnia - 2013/2014
|
 Zadania tygodnia - 2014/2015
Zadania tygodnia - 2014/2015
 Zadania tygodnia
- 2015/2016
Zadania tygodnia
- 2015/2016
 Zadania tygodnia
- 2016/2017
Zadania tygodnia
- 2016/2017
 Zadania tygodnia
- 2017/2018
Zadania tygodnia
- 2017/2018
 Zadania tygodnia
- 2018/2019
Zadania tygodnia
- 2018/2019
 Zadania tygodnia
- 2019/2020
Zadania tygodnia
- 2019/2020
 Zadania tygodnia
- 2020/2021
Zadania tygodnia
- 2020/2021
 Zadania tygodnia
- 2021/2022
Zadania tygodnia
- 2021/2022
 Zadania tygodnia
- 2022/2023
Zadania tygodnia
- 2022/2023
 Zadania tygodnia
- 2023/2024
Zadania tygodnia
- 2023/2024 |
Zadania tygodnia kierowane są do wszystkich zainteresowanych uczniów kl. I-III
szkół podstawowych.
|
|

|
| .Zadanie
nr 1. |
|
 Ile
jest takich trzycyfrowych liczb, które można ułożyć z cyfr 3, 4, 5? W
każdej z liczb należy wykorzystać wszystkie trzy cyfry. Ile
jest takich trzycyfrowych liczb, które można ułożyć z cyfr 3, 4, 5? W
każdej z liczb należy wykorzystać wszystkie trzy cyfry.
|
|
Zwycięzca konkursu: Bella
Hainutdinova
uczennica klasy: trzeciej
"g"
ze
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie
nr 2. |
|
 Dziadek
lubił się zamieniać. Na początku miał on torbę złota, którą zamienił na
dwa konie. Każdego konia zamienił na dwie kozy. Każdą kozę zamienił na
dwie kury. Za każdą kurę dziadek otrzymał jeden kwiat z trzema płatkami.
Ile kwiatowych płatków miał dziadek? Dziadek
lubił się zamieniać. Na początku miał on torbę złota, którą zamienił na
dwa konie. Każdego konia zamienił na dwie kozy. Każdą kozę zamienił na
dwie kury. Za każdą kurę dziadek otrzymał jeden kwiat z trzema płatkami.
Ile kwiatowych płatków miał dziadek? |
|
Zwycięzca konkursu: Rafał
Wiśliński
uczeń klasy: trzeciej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 3. |
|
 Na
lekcji WF dziewczynki dzieliły się na grupy. Gdy tworzyły grupy
trzyosobowe, zostawała jedna dziewczynka. Gdy tworzyły grupy
czteroosobowe, to też zostawała jedna dziewczynka. Ile dziewczynek
ćwiczyło na tej lekcji, jeżeli wiadomo, że było ich mniej niż 20? Na
lekcji WF dziewczynki dzieliły się na grupy. Gdy tworzyły grupy
trzyosobowe, zostawała jedna dziewczynka. Gdy tworzyły grupy
czteroosobowe, to też zostawała jedna dziewczynka. Ile dziewczynek
ćwiczyło na tej lekcji, jeżeli wiadomo, że było ich mniej niż 20? |
|
Zwycięzca konkursu: Maja
Krzemińska
uczennica klasy: trzeciej
"a"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 4. |
|
 Szachownicę
o wymiarach 3x3 chcemy rozciąć (nie przecinając żadnego pola) na
trzy części tak, by każda część składała się z innej liczby pół i by
każda część składała się przynajmniej z dwóch pól. Z ilu pól
będzie złożony największy z otrzymanych kawałków? Szachownicę
o wymiarach 3x3 chcemy rozciąć (nie przecinając żadnego pola) na
trzy części tak, by każda część składała się z innej liczby pół i by
każda część składała się przynajmniej z dwóch pól. Z ilu pól
będzie złożony największy z otrzymanych kawałków? |
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
września
wylosował:
Milan Baran
uczeń:
klasy trzeciej "b"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie
|
|

|
|
Zadanie
nr 5. |
|
 Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i podaj odpowiedź. Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i podaj odpowiedź.
23 - 15 + 9 =….. |
|
Zwycięzca konkursu: Julia
Lipa
uczennica klasy: trzeciej
"a"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 6. |
|
 Czy
potrafisz wyjaśnić następującą sytuację: Dwóch ojców i dwóch synów
podzielili się 3 jabłkami i każdy otrzymał po 1 całym jabłku. Czy
potrafisz wyjaśnić następującą sytuację: Dwóch ojców i dwóch synów
podzielili się 3 jabłkami i każdy otrzymał po 1 całym jabłku. |
|
Zwycięzca konkursu: Tomasz
Kawka
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie
nr 7. |
|
 Samochód
jadący ze stałą prędkością pokonuje 72 km w ciągu godziny. Jaką
odległość przejedzie w ciągu sekundy? Samochód
jadący ze stałą prędkością pokonuje 72 km w ciągu godziny. Jaką
odległość przejedzie w ciągu sekundy? |
|
Zwycięzca konkursu: Ignacy
Ulaniuk
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie
nr 8. |
 Na stacji początkowej do pustego pociągu wsiadło 93 pasażerów. Na
pierwszej stacji wysiadło 85, a wsiadło 43 pasażerów. Na następnej –
wsiadły 3 grupy dzieci: I- 13 dzieci, II –15 dzieci, III – 18 dzieci.
Ile teraz osób jedzie w pociągu?
Na stacji początkowej do pustego pociągu wsiadło 93 pasażerów. Na
pierwszej stacji wysiadło 85, a wsiadło 43 pasażerów. Na następnej –
wsiadły 3 grupy dzieci: I- 13 dzieci, II –15 dzieci, III – 18 dzieci.
Ile teraz osób jedzie w pociągu? |
|
Zwycięzca konkursu: Milan
Baran
uczeń klasy: trzeciej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
października
wylosowała:
Marta Orchowska
uczennica:
klasy drugiej "b"
ze
Szkoły Podstawowej
nr
5
im. Króla Władysława Łokietka
w
Lublinie
|
|

|
|
Zadanie
nr 9. |
 Ile
najwięcej piątków może wypaść w ciągu roku? Ile
najwięcej piątków może wypaść w ciągu roku? |
|
Zwycięzca konkursu: Małgorzata
Mastalerz
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 10. |
|
 Drużyna
harcerska wybrała się na trzydniowy biwak. Pierwszego dnia harcerze
przebyli trasę 18 km. Drugiego dnia ich trasa była o 6 km krótsza. W
trzecim dniu pokonali trasę o 5 km dłuższą niż drugiego dnia. Ile km
przeszli harcerze w ciągu trzech dni? Drużyna
harcerska wybrała się na trzydniowy biwak. Pierwszego dnia harcerze
przebyli trasę 18 km. Drugiego dnia ich trasa była o 6 km krótsza. W
trzecim dniu pokonali trasę o 5 km dłuższą niż drugiego dnia. Ile km
przeszli harcerze w ciągu trzech dni? |
|
Zwycięzca konkursu: Aleksander
Żur
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 11. |
|
 Jacek
jest trzy razy starszy od Andrzeja, a Andrzej jest o 8 lat młodszy
od Jacka. Ile lat mają łącznie obaj chłopcy? Jacek
jest trzy razy starszy od Andrzeja, a Andrzej jest o 8 lat młodszy
od Jacka. Ile lat mają łącznie obaj chłopcy? |
|
Zwycięzca konkursu: Paweł
Trocewicz
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 12. |
|
 Na
stole stoi 6 pudełek, w każdym z nich znajduje się 6 woreczków, a w
każdym z woreczków jest 6 ziarenek ryżu. Ile ziarenek ryżu jest
łącznie we wszystkich woreczkach? Na
stole stoi 6 pudełek, w każdym z nich znajduje się 6 woreczków, a w
każdym z woreczków jest 6 ziarenek ryżu. Ile ziarenek ryżu jest
łącznie we wszystkich woreczkach?
|
|
Zwycięzca konkursu: Zuzanna
Pszenny
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
listopada
wylosowała:
Milena Rębacz
uczennica:
klasy trzeciej "a"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie
|
|

|
|
Zadanie
nr 13. |
|
 Edward
zdobył wszystkie bramki dla drużyny „Smoków” w meczu piłkarskim, w
którym „Smoki zmierzyły się z „Tygrysami”. W drużynie „Tygrysów
bramki strzelali: Bartek – połowę tego, co Edward, i Norbert o 2
bramki mniej od Edwarda. Jakim wynikiem zakończył się mecz, jeśli
wiadomo, że Edward strzelił 6 bramek? Edward
zdobył wszystkie bramki dla drużyny „Smoków” w meczu piłkarskim, w
którym „Smoki zmierzyły się z „Tygrysami”. W drużynie „Tygrysów
bramki strzelali: Bartek – połowę tego, co Edward, i Norbert o 2
bramki mniej od Edwarda. Jakim wynikiem zakończył się mecz, jeśli
wiadomo, że Edward strzelił 6 bramek? |
|
Zwycięzca konkursu: Anna
Domańska
uczennica klasy: trzeciej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 14. |
|
 W
pewnym budynku znajduje się 8 mieszkań. Każde z nich to
mieszkanie 2-pokojowe lub 3-pokojowe i łącznie mają one 18 pokoi. O
ile więcej jest mieszkań 2-pokojowych niż mieszkań 3-pokojowych? W
pewnym budynku znajduje się 8 mieszkań. Każde z nich to
mieszkanie 2-pokojowe lub 3-pokojowe i łącznie mają one 18 pokoi. O
ile więcej jest mieszkań 2-pokojowych niż mieszkań 3-pokojowych? |
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie
nr 15. |
|
 Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i podaj odpowiedź. Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i podaj odpowiedź.
□
+ 17- 46 = 43 |
|
Zwycięzca konkursu: Mikołaj
Zarych
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 16. |
|
 Staszek
ma dwukrotnie mniej złotówek niż dwuzłotówek i trzykrotnie mniej
złotówek niż pięciozłotówek. Łącznie ma 12 monet w trzech
nominałach. Ile ma pieniędzy? Staszek
ma dwukrotnie mniej złotówek niż dwuzłotówek i trzykrotnie mniej
złotówek niż pięciozłotówek. Łącznie ma 12 monet w trzech
nominałach. Ile ma pieniędzy? |
|
Zwycięzca konkursu: Antoni
Gawda
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 17. |
|
 Żaby
i ropuchy to pożyteczne zwierzęta, żyjące na naszych działkach.
Żywią się one szkodnikami hodowanych roślin. Obecność na działce
jednej żaby lub ropuchy może podnieść plony o ¼. Na poletku
truskawek na działce Marysi grasują szkodniki. Plony wynoszą 128 kg.
Oblicz, jakie byłyby plony truskawek, gdyby szkodniki były zjadane
przez żabę lub ropuchę. Żaby
i ropuchy to pożyteczne zwierzęta, żyjące na naszych działkach.
Żywią się one szkodnikami hodowanych roślin. Obecność na działce
jednej żaby lub ropuchy może podnieść plony o ¼. Na poletku
truskawek na działce Marysi grasują szkodniki. Plony wynoszą 128 kg.
Oblicz, jakie byłyby plony truskawek, gdyby szkodniki były zjadane
przez żabę lub ropuchę. |
|
Zwycięzca konkursu: Michał Zarych
uczeń klasy: trzeciej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
grudnia
wylosował:
Jakub Furlepa
uczeń:
klasy drugiej "b"
ze
Szkoły Podstawowej
nr
5
im. Króla Władysława Łokietka
w
Lublinie
|
|

|
|
Zadanie nr 18. |
|
 W
klasie Agnieszki jest dwukrotnie więcej dziewcząt niż chłopców. O
ile mniejsza jest liczba chłopców od liczby dziewcząt w tej klasie,
jeśli łącznie jest w niej 21 uczniów? W
klasie Agnieszki jest dwukrotnie więcej dziewcząt niż chłopców. O
ile mniejsza jest liczba chłopców od liczby dziewcząt w tej klasie,
jeśli łącznie jest w niej 21 uczniów? |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 19. |
|
 Między
cyfry 333333 wstaw po jednym znaku każdego z działań tak, aby otrzymać w
wyniku liczbę 5. Między
cyfry 333333 wstaw po jednym znaku każdego z działań tak, aby otrzymać w
wyniku liczbę 5. |
|
Zwycięzca konkursu: Julia
Lipa
uczennica klasy: trzeciej
"a"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 20. |
|
 Jacek
ma kilka dwuzłotówek, a Bartek ma tyle samo pieniędzy co Jacek, ale
w pięciozłotówkach. Ile łącznie monet mają obaj chłopcy? Jacek
ma kilka dwuzłotówek, a Bartek ma tyle samo pieniędzy co Jacek, ale
w pięciozłotówkach. Ile łącznie monet mają obaj chłopcy? |
|
Zwycięzca konkursu: Wojciech
Wieczorek
uczeń klasy: trzeciej
"a"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 21. |
|
 Józek
miał 28 zł. Postanowił je wrzucić do trzech skarbonek tak, aby w
drugiej skarbonce było dwa razy więcej pieniędzy, niż w pierwszej, a
w trzeciej dwa razy więcej pieniędzy niż w drugiej. Oblicz, ile
pieniędzy Józek włożył do każdej skarbonki? Józek
miał 28 zł. Postanowił je wrzucić do trzech skarbonek tak, aby w
drugiej skarbonce było dwa razy więcej pieniędzy, niż w pierwszej, a
w trzeciej dwa razy więcej pieniędzy niż w drugiej. Oblicz, ile
pieniędzy Józek włożył do każdej skarbonki?



|
|
Zwycięzca konkursu: Kamila
Wikieta
uczennica klasy: trzeciej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
stycznia
wylosowała:
Natalia Pachała
uczennica:
klasy trzeciej "g"
ze
Szkoły Podstawowej
nr
14
im. Tadeusza Kościuszki
w
Lublinie
|
|

|
|
Zadanie nr 22. |
|
 W
ogrodzie zoologicznym Bolek po raz pierwszy zobaczył kangury.
Zauważył, że każdy kangur ma cztery łapy, dwoje uszu i jeden ogon.
Dla zabawy policzył łączną liczbę łap, uszu i ogonów otrzymując w
wyniku 63. Ile kangurów było na wybiegu? W
ogrodzie zoologicznym Bolek po raz pierwszy zobaczył kangury.
Zauważył, że każdy kangur ma cztery łapy, dwoje uszu i jeden ogon.
Dla zabawy policzył łączną liczbę łap, uszu i ogonów otrzymując w
wyniku 63. Ile kangurów było na wybiegu? |
|
Zwycięzca konkursu: Stella
Tabor
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 23. |
 Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i napisz odpowiedź. Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i napisz odpowiedź.
g
+ ( 8 ∙ 17) = 831 |
|
Zwycięzca konkursu: Katarzyna
Lizak
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 24. |
|
 Janek
próbował tak rozmieścić nawiasy w działaniu 6 . 8
+ 20 : 4 - 2, aby otrzymać wynik 58. Który sposób jest poprawny? Janek
próbował tak rozmieścić nawiasy w działaniu 6 . 8
+ 20 : 4 - 2, aby otrzymać wynik 58. Który sposób jest poprawny?
a) 6
. (8 +20) : 4 - 2
b) (6
. 8 + 20 : 4) - 2
c) (6
. 8 + 20) : 4 - 2
d) 6
. 8 + 20 : (4 - 2)
e) 6
. (8 + 20 : 4) - 2 |
|
Zwycięzca konkursu: Bella
Hainutdinova
uczennica klasy: trzeciej
"g"
ze
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 25. |
|
 Dwaj
chłopcy szli z domu do szkoły i spotkali po drodze jeszcze 5
chłopców. Ilu chłopców szło z domu do szkoły? Dwaj
chłopcy szli z domu do szkoły i spotkali po drodze jeszcze 5
chłopców. Ilu chłopców szło z domu do szkoły? |
|
Zwycięzca konkursu: Pola
Skwarcz
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
lutego
wylosował:
Wojciech Kocki
uczeń:
klasy drugiej "b"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 26. |
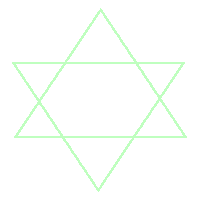
 Ile
trójkątów dostrzegasz na tym rysunku? Ile
trójkątów dostrzegasz na tym rysunku?
|
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie nr 27. |
|
 Leciały
gęsi: jedna gęś na przodzie, a 2 z tyłu, 1 z tyłu i dwie na przodzie,
1 między dwiema i 3 w jednym rzędzie. Ile było wszystkich gęsi? Leciały
gęsi: jedna gęś na przodzie, a 2 z tyłu, 1 z tyłu i dwie na przodzie,
1 między dwiema i 3 w jednym rzędzie. Ile było wszystkich gęsi? |
|
Zwycięzca konkursu: Alicja
Barańska
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 28. |
|
 Marysia
mieszka w wieżowcu w mieszkaniu nr 17. Parter domu zajmują sklepy.
Na każdym piętrze, począwszy od pierwszego, znajdują sie 3
mieszkania. Na którym piętrze mieszka Marysia? Marysia
mieszka w wieżowcu w mieszkaniu nr 17. Parter domu zajmują sklepy.
Na każdym piętrze, począwszy od pierwszego, znajdują sie 3
mieszkania. Na którym piętrze mieszka Marysia? |
|
Zwycięzca konkursu: Wojciech
Wieczorek
uczeń klasy: trzeciej
"a"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 29. |
|
 Pokój
ma 4 kąty. W każdym kącie siedzi kot. Naprzeciw każdego kota siedzą
3 koty. Ile jest wszystkich kotów w pokoju? Pokój
ma 4 kąty. W każdym kącie siedzi kot. Naprzeciw każdego kota siedzą
3 koty. Ile jest wszystkich kotów w pokoju? |
|
Zwycięzca konkursu: Weronika
Żydek
uczennica klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 30. |
|
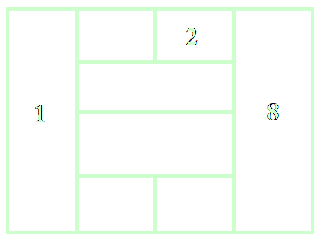
 Mariola
zamierza wpisać
w taki sposób, aby liczby wpisane w pola sąsiadujące różniły się co
najmniej o 2. Trzy liczby już wpisała. Wpisz pozostałe pięć liczb. Mariola
zamierza wpisać
w taki sposób, aby liczby wpisane w pola sąsiadujące różniły się co
najmniej o 2. Trzy liczby już wpisała. Wpisz pozostałe pięć liczb.
|
|
Zwycięzca konkursu: Katarzyna
Lizak
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
marca
wylosował:
Stanisław Gieroba
uczeń:
klasy trzeciej "a"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 31. |
|
 Jaką
liczbę należy umieścić w miejsce x, aby zachodziła równość: Jaką
liczbę należy umieścić w miejsce x, aby zachodziła równość:
12 .
12 . 12 = 6 . x
. 6 ?
|
|
Zwycięzca konkursu: Anna
Woźniak
uczennica klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
15 im.
Jana Pawła II w
Lublinie
|
|
Zadanie nr 32. |
|
 Dwóch
chłopców znalazło na drodze 8 złotych. Ile pieniędzy znajdzie pięciu
chłopców? Dwóch
chłopców znalazło na drodze 8 złotych. Ile pieniędzy znajdzie pięciu
chłopców?
|
|
Zwycięzca konkursu: Bella
Hainutdinova
uczennica klasy: trzeciej
"g"
ze
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 33. |
|
 Marta
ma o dwa długopisy mniej od Agaty, Agata ma dwa razy więcej
długopisów niż Julia, a Julia ma o 3 długopisy mniej od Marty. Ile
długopisów ma Agata? Marta
ma o dwa długopisy mniej od Agaty, Agata ma dwa razy więcej
długopisów niż Julia, a Julia ma o 3 długopisy mniej od Marty. Ile
długopisów ma Agata? |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 34. |
|
 Ile
liczb trzycyfrowych możesz utworzyć przy pomocy cyfr 3, 0, 7, używając
każdej z nich dokładnie jeden raz? Ile
liczb trzycyfrowych możesz utworzyć przy pomocy cyfr 3, 0, 7, używając
każdej z nich dokładnie jeden raz? |
|
Zwycięzca konkursu: Mikołaj
Zarych
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
kwietnia
wylosował:
Szymon Cioch
uczeń:
klasy drugiej "b"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 35. |
 U
rąk jest 10 palców. Ile palców jest u 10 rąk? U
rąk jest 10 palców. Ile palców jest u 10 rąk? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|
Zadanie nr 36. |
|
 W
kratki papierowej taśmy W
kratki papierowej taśmy
należy wpisać liczby całkowite od 1 do 10 w takiej kolejności, aby
każda wpisana liczba począwszy od drugiej była większa o 3 albo
mniejsza o 2 od liczby wpisanej w poprzedniej kratce. Liczba 6
została juz wpisana na pozycji siódmej.
|
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie nr 37. |
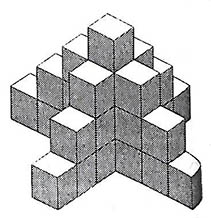
 Z
ilu klocków zbudowana jest ta wieża? Z
ilu klocków zbudowana jest ta wieża?
|
|
Zwycięzca konkursu: Antoni
Gawda
uczeń klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 38. |
 Ile końców
mają 3 kije, pięć kijów i pół kija? Ile końców
mają 3 kije, pięć kijów i pół kija? |
|
Zwycięzca konkursu: Katarzyna
Lizak
uczennica klasy: drugiej
"b"
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
maja
wylosowała:
Helena Ukalska
uczeń:
klasy trzeciej "a"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 39. |
 Szlaczek
złożony jest z odcinków. Początkowy fragment tego szlaczka pokazano
na rysunku: Szlaczek
złożony jest z odcinków. Początkowy fragment tego szlaczka pokazano
na rysunku:
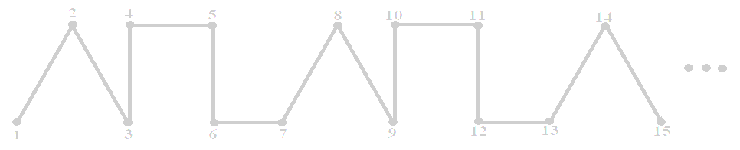
Punkt początkowy szlaczka oraz punkty, w których łączą się odcinki
ponumerowano kolejnymi liczbami naturalnymi. Narysuj fragment tego
szlaczka rozpoczynający się punktem 2000 i zakończony punktem 2006. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 40. |
 Ślimak
wspina się na drzewo wysokości 10 m w ciągu dnia podnosi sie o 4 m,
a w ciągu nocy obsuwa się o 3 m. Po ilu dniach ślimak dostał się na
wierzchołek drzewa? Ślimak
wspina się na drzewo wysokości 10 m w ciągu dnia podnosi sie o 4 m,
a w ciągu nocy obsuwa się o 3 m. Po ilu dniach ślimak dostał się na
wierzchołek drzewa? |
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie nr 41. |
|
 Posadzka
wyłożona jest kafelkami jednakowego kształtu. Każdy kawałek złożony
jest z trzech jednakowych elementów, rys 1. Posadzka
wyłożona jest kafelkami jednakowego kształtu. Każdy kawałek złożony
jest z trzech jednakowych elementów, rys 1.
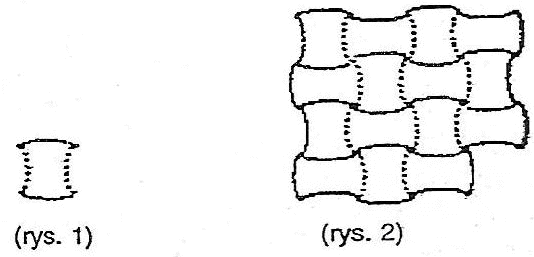
Fragment posadzki, pokazany na rys. 2, złożony jest z 5 kafelków.
Zaznacz brzegi tych kafelków. |
|
Zwycięzca konkursu: Antoni
Rząd
uczeń klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
5 im.
Króla Władysława Łokietka w
Lublinie
|
|
Zadanie nr 42. |
|
 Kangur
przebywa drogę od startu do mety po odcinkach przedstawionego diagramu.
Obok każdego odcinka podany jest czas (w minutach) potrzebny na
przebycie tego odcinka. Jaki jest najkrótszy czas dotarcia do mety? Kangur
przebywa drogę od startu do mety po odcinkach przedstawionego diagramu.
Obok każdego odcinka podany jest czas (w minutach) potrzebny na
przebycie tego odcinka. Jaki jest najkrótszy czas dotarcia do mety?

|
|
Zwycięzca konkursu: Anna
Woźniak
uczennica klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
15 im.
Jana Pawła II w
Lublinie
|
|
Zadanie nr 43. |
|
 Przyleciały
kawki i siadły na ławki. Gdyby na każdej ławce siadło po jednej
kawce, zabrakłoby jednej ławki. Gdyby zaś na każdej ławce siadły
dwie kawki, jedna ławka byłaby pusta. Ile było ławek i ile kawek? Przyleciały
kawki i siadły na ławki. Gdyby na każdej ławce siadło po jednej
kawce, zabrakłoby jednej ławki. Gdyby zaś na każdej ławce siadły
dwie kawki, jedna ławka byłaby pusta. Ile było ławek i ile kawek? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
czerwca
wylosował:
Mikołaj Zarych
uczeń:
klasy drugiej "b"
ze
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 44. |
|
 Łukasz
zamyka swoje skarby zamkiem używając jednego z posiadanych szyfrów
sześciocyfrowych. Szyfry Łukasza są liczbami, w których każda z cyfr
spośród: 1, 2, 3, 4, 5 i 6 występuje dokładnie jeden raz i w których -
licząc od strony lewej - dwie pierwsze cyfry tworzą liczbę dwucyfrową
podzielną przez 2, trzy pierwsze cyfry tworzą liczbę trzycyfrową
podzielną przez 3, itd.; w końcu wszystkie cyfry tworzą liczbę
sześciocyfrową podzielną przez 6. Ile różnych szyfrów ma Łukasz? Jeśli
ma więcej niż jeden, to podaj również dwa z nich. Łukasz
zamyka swoje skarby zamkiem używając jednego z posiadanych szyfrów
sześciocyfrowych. Szyfry Łukasza są liczbami, w których każda z cyfr
spośród: 1, 2, 3, 4, 5 i 6 występuje dokładnie jeden raz i w których -
licząc od strony lewej - dwie pierwsze cyfry tworzą liczbę dwucyfrową
podzielną przez 2, trzy pierwsze cyfry tworzą liczbę trzycyfrową
podzielną przez 3, itd.; w końcu wszystkie cyfry tworzą liczbę
sześciocyfrową podzielną przez 6. Ile różnych szyfrów ma Łukasz? Jeśli
ma więcej niż jeden, to podaj również dwa z nich. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 45. |
|
 Joasia
upiekła kilkanaście ciasteczek. Próbowała je rozmieścić w równych
ilościach najpierw na dwóch talerzykach, potem na trzech talerzykach i
wreszcie na czterech talerzykach. za każdym razem zostawało jedno
ciasteczko. Która z liczb: 9, 10, 11, 12 i 13 wyraża ilość upieczonych
ciasteczek? Joasia
upiekła kilkanaście ciasteczek. Próbowała je rozmieścić w równych
ilościach najpierw na dwóch talerzykach, potem na trzech talerzykach i
wreszcie na czterech talerzykach. za każdym razem zostawało jedno
ciasteczko. Która z liczb: 9, 10, 11, 12 i 13 wyraża ilość upieczonych
ciasteczek? |
|
Zwycięzca konkursu: Anna
Woźniak
uczennica klasy: pierwszej
"b"
ze
Szkoły Podstawowej nr
15 im.
Jana Pawła II w
Lublinie
|
|
Zadanie nr 46. |
 Na
polu siedziało 15 kuropatw. Myśliwy strzelił i zabił 5. Ile
pozostało? Na
polu siedziało 15 kuropatw. Myśliwy strzelił i zabił 5. Ile
pozostało? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|
Zadanie nr 47. |
|
 Skoczki
A i B poruszają się po wspólnej prostej. Skoczek A wykonuje skoki
długości 4 m, każdy skok w czasie 2 sekund i po każdym skoku
odpoczywa 1 sekundę. Skoczek B wykonuje skoki długości 3 m, każdy
skok w czasie 1 sekundy i nie odpoczywa między skokami. Skoczek B
znajduje się w odległości 32 m od skoczka A, którego ściga. Może
złapać go tylko wtedy, gdy znajdzie się na prostej w tym samym
punkcie w którym skoczek A odpoczywa. Po ilu sekundach, od wspólnego
startu, skoczek B złapie skoczka A? Skoczki
A i B poruszają się po wspólnej prostej. Skoczek A wykonuje skoki
długości 4 m, każdy skok w czasie 2 sekund i po każdym skoku
odpoczywa 1 sekundę. Skoczek B wykonuje skoki długości 3 m, każdy
skok w czasie 1 sekundy i nie odpoczywa między skokami. Skoczek B
znajduje się w odległości 32 m od skoczka A, którego ściga. Może
złapać go tylko wtedy, gdy znajdzie się na prostej w tym samym
punkcie w którym skoczek A odpoczywa. Po ilu sekundach, od wspólnego
startu, skoczek B złapie skoczka A? |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|

|
|
 Uwaga!:
nagrodę-niespodziankę
miesiąca
lipca
Uwaga!:
nagrodę-niespodziankę
miesiąca
lipca
wylosowała:
Anna Woźniak
uczeń:
klasy pierwszej "b"
ze
Szkoły Podstawowej
nr
15
im. Jana Pawła II
w
Lublinie |
|

|
|
Zadanie nr 48. |
|
 Wybrałem
pewną liczbę. Odjąłem od niej 40, następnie do otrzymanego wyniku
dodałem 2000 i w rezultacie otrzymałem 3250. jaką liczbę wybrałem na
początku? Wybrałem
pewną liczbę. Odjąłem od niej 40, następnie do otrzymanego wyniku
dodałem 2000 i w rezultacie otrzymałem 3250. jaką liczbę wybrałem na
początku? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|
Zadanie nr 49. |
|
 O
to trzy pigułki - mówi lekarz choremu - niech pan od zaraz przyjmuje
je po jednej pigułce co pół godziny. Na jak długo wystarczy choremu
tych pigułek? O
to trzy pigułki - mówi lekarz choremu - niech pan od zaraz przyjmuje
je po jednej pigułce co pół godziny. Na jak długo wystarczy choremu
tych pigułek? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|
Zadanie nr 50. |
|
 Mając
pełny zestaw 28 kostek domina (od 0-0 do 6-6) możemy budować -
zgodnie z zasadami tej gry - różne zamknięte łańcuchy. Przykład
takiego łańcucha złożonego z 10 kostek pokazany jest na rysunku
poniżej. Beata ma zdekompletowany zestaw, w którym brakuje trzech
kostek: 0-1, 0-2 i 0-3. Wykorzystując odpowiednie kostki swego
zestawu zbudowała łańcuch zamknięty najdłuższy z możliwych. Z ilu
kostek składał się ten łańcuch? Mając
pełny zestaw 28 kostek domina (od 0-0 do 6-6) możemy budować -
zgodnie z zasadami tej gry - różne zamknięte łańcuchy. Przykład
takiego łańcucha złożonego z 10 kostek pokazany jest na rysunku
poniżej. Beata ma zdekompletowany zestaw, w którym brakuje trzech
kostek: 0-1, 0-2 i 0-3. Wykorzystując odpowiednie kostki swego
zestawu zbudowała łańcuch zamknięty najdłuższy z możliwych. Z ilu
kostek składał się ten łańcuch?

|
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 51. |
|
 Ślimak
wpadł w poniedziałek rano do studni o głębokości 5 metrów. W
ciągu dnia ślimak wspina się na wysokość 2 m, w ciągu nocy zaś
ześlizguje się w dół o 1 m. W którym dniu tygodnia ślimak wydostanie się
ze studni? Ślimak
wpadł w poniedziałek rano do studni o głębokości 5 metrów. W
ciągu dnia ślimak wspina się na wysokość 2 m, w ciągu nocy zaś
ześlizguje się w dół o 1 m. W którym dniu tygodnia ślimak wydostanie się
ze studni? |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
adanie nr 52. |
|
 Dwóch
chłopców urodziło się w tym samym dniu i w tym samym roku, u tych samych
rodziców, mimo to nie byli bliźniętami. Czy jest to możliwe? Dwóch
chłopców urodziło się w tym samym dniu i w tym samym roku, u tych samych
rodziców, mimo to nie byli bliźniętami. Czy jest to możliwe? |
|
Zwycięzca konkursu: Wojciech
Sawczyk
uczeń klasy: drugiej
"a"
ze
Szkoły Podstawowej nr
2 im.
Marszałka Józefa Piłsudskiego w
Tomaszowie Lubelskim
|
|

|
|
Nagrodę roku szkolnego
2019/2020
wylosowała:
Lidia Rak
uczennica:
klasy drugiej b
ze
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Gratulujemy
Zwycięzcom
i zapraszamy
do udziału w konkursie
"Zadań tygodnia"
w Nowym Roku Szkolnym 2020/2021. |
|
|

 Powrót na stronę główną
Powrót na stronę główną |
 Na stacji początkowej do pustego pociągu wsiadło 93 pasażerów. Na
pierwszej stacji wysiadło 85, a wsiadło 43 pasażerów. Na następnej –
wsiadły 3 grupy dzieci: I- 13 dzieci, II –15 dzieci, III – 18 dzieci.
Ile teraz osób jedzie w pociągu?
Na stacji początkowej do pustego pociągu wsiadło 93 pasażerów. Na
pierwszej stacji wysiadło 85, a wsiadło 43 pasażerów. Na następnej –
wsiadły 3 grupy dzieci: I- 13 dzieci, II –15 dzieci, III – 18 dzieci.
Ile teraz osób jedzie w pociągu? Ile
najwięcej piątków może wypaść w ciągu roku?
Ile
najwięcej piątków może wypaść w ciągu roku? Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i napisz odpowiedź.
Do
podanego działania ułóż treść zadania, postaw pytanie. Rozwiąż
działanie i napisz odpowiedź. Ile
trójkątów dostrzegasz na tym rysunku?
Ile
trójkątów dostrzegasz na tym rysunku? U
rąk jest 10 palców. Ile palców jest u 10 rąk?
U
rąk jest 10 palców. Ile palców jest u 10 rąk? Z
ilu klocków zbudowana jest ta wieża?
Z
ilu klocków zbudowana jest ta wieża? Ile końców
mają 3 kije, pięć kijów i pół kija?
Ile końców
mają 3 kije, pięć kijów i pół kija? Szlaczek
złożony jest z odcinków. Początkowy fragment tego szlaczka pokazano
na rysunku:
Szlaczek
złożony jest z odcinków. Początkowy fragment tego szlaczka pokazano
na rysunku: Ślimak
wspina się na drzewo wysokości 10 m w ciągu dnia podnosi sie o 4 m,
a w ciągu nocy obsuwa się o 3 m. Po ilu dniach ślimak dostał się na
wierzchołek drzewa?
Ślimak
wspina się na drzewo wysokości 10 m w ciągu dnia podnosi sie o 4 m,
a w ciągu nocy obsuwa się o 3 m. Po ilu dniach ślimak dostał się na
wierzchołek drzewa? Na
polu siedziało 15 kuropatw. Myśliwy strzelił i zabił 5. Ile
pozostało?
Na
polu siedziało 15 kuropatw. Myśliwy strzelił i zabił 5. Ile
pozostało?







