|
 |
Archiwum zadań
tygodnia 2016-2017
 |
|
|
 Zadania tygodnia - 2003/2004
Zadania tygodnia - 2003/2004
 Zadania tygodnia - 2004/2005
Zadania tygodnia - 2004/2005
 Zadania tygodnia - 2005/2006
Zadania tygodnia - 2005/2006
 Zadania tygodnia - 2006/2007
Zadania tygodnia - 2006/2007
 Zadania tygodnia - 2007/2008
Zadania tygodnia - 2007/2008
 Zadania tygodnia - 2008/2009
Zadania tygodnia - 2008/2009
 Zadania tygodnia - 2009/2010
Zadania tygodnia - 2009/2010
 Zadania tygodnia - 2010/2011
Zadania tygodnia - 2010/2011
 Zadania tygodnia - 2011/2012
Zadania tygodnia - 2011/2012
 Zadania tygodnia - 2012/2013
Zadania tygodnia - 2012/2013
 Zadania tygodnia - 2013/2014
Zadania tygodnia - 2013/2014 |
 Zadania tygodnia - 2014/2015
Zadania tygodnia - 2014/2015
 Zadania tygodnia
- 2015/2016
Zadania tygodnia
- 2015/2016
 Zadania tygodnia
- 2016/2017
Zadania tygodnia
- 2016/2017
 Zadania tygodnia
- 2017/2018
Zadania tygodnia
- 2017/2018
 Zadania tygodnia
- 2018/2019
Zadania tygodnia
- 2018/2019
 Zadania tygodnia
- 2019/2020
Zadania tygodnia
- 2019/2020
 Zadania tygodnia
- 2020/2021
Zadania tygodnia
- 2020/2021
 Zadania tygodnia
- 2021/2022
Zadania tygodnia
- 2021/2022
 Zadania tygodnia
- 2022/2023
Zadania tygodnia
- 2022/2023
 Zadania tygodnia
- 2023/2024
Zadania tygodnia
- 2023/2024 |
|
Zadania tygodnia kierowane są do wszystkich zainteresowanych uczniów kl. I-III
szkół podstawowych.
|
|

|
| .Zadanie
nr 1. |
|
 Znajdź
największą liczbę dziesięciocyfrową składająca się z różnych cyfr.
Znajdź
największą liczbę dziesięciocyfrową składająca się z różnych cyfr.
|
|
Zwycięzca konkursu: Filip
Tolarz
uczeń klasy: trzeciej
z
Zespołu Szkolno-Przedszkolnego nr
1,
Szkoły Podstawowej nr
16 im.
Adama Dzika w
Wodzisławiu Śląskim
|
|
Zadanie
nr 2. |
|
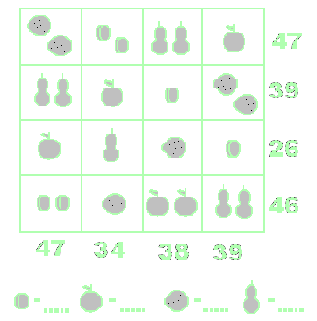
 Przyjrzyj
się uważnie tabeli i odkryj, jakie liczby kryją się pod
poszczególnymi owocami. Przyjrzyj
się uważnie tabeli i odkryj, jakie liczby kryją się pod
poszczególnymi owocami.
|
|
Zwycięzca konkursu: Dagmara
Woźniak
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 3. |
|
 Mama
Agaty pracuje w biurze. Dzisiaj będzie potrzebowała 569 spinaczy.
Ile musi mieć pudełek ze spinaczami, jeśli w każdym jest 100 sztuk? Mama
Agaty pracuje w biurze. Dzisiaj będzie potrzebowała 569 spinaczy.
Ile musi mieć pudełek ze spinaczami, jeśli w każdym jest 100 sztuk? |
|
Zwycięzca konkursu: Igor
Kujawski
uczeń klasy: trzeciej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 4. |
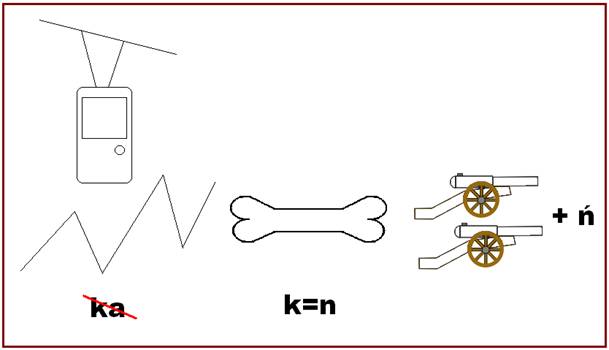
 Rozwiąż
rebus: Rozwiąż
rebus:
|
|
Zwycięzca konkursu: Aleksandra
Lech
uczennica klasy: drugiej
"b"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
września
wylosował:
Miłosz Daniewski
uczeń:
klasy trzeciej "a"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie
nr 5. |
|
 Martyna
miała w skarbonce 94 zł. Dała bratu 56 zł, a za pozostałe pieniądze
kupiła 2 jednakowe piórniki. Ile kosztował piórnik? Martyna
miała w skarbonce 94 zł. Dała bratu 56 zł, a za pozostałe pieniądze
kupiła 2 jednakowe piórniki. Ile kosztował piórnik? |
|
Zwycięzca konkursu: Aleksandra
Brelik
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie
nr 6. |
|
 Uzupełnij
zdania. Uzupełnij
zdania.
Trójkąt równoramienny, w którym kąt przy podstawie ma miarę 45o,
jest trójkątem ................................ . W trójkącie
................................. wszystkie wysokości leżą wewnątrz
tego trójkąta. Krótsza przekątna rombu, w którym jeden z kątów ma
120o, dzieli go na dwa trójkąty
................................... . Czworokąt, w którym przekątne
dzielą się na połowy to ............................. .
|
|
Zwycięzca konkursu: Emilia
Markowska
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 7. |
|
 Piechur
potrzebuje 12 minut, aby obejść dookoła kwadratowy plac. Ile minut
zajmuje mu obejście w tym samym tempie dookoła kwadratowego placu o
powierzchni 4 razy większej. Piechur
potrzebuje 12 minut, aby obejść dookoła kwadratowy plac. Ile minut
zajmuje mu obejście w tym samym tempie dookoła kwadratowego placu o
powierzchni 4 razy większej. |
|
Zwycięzca konkursu: Zofia
Jastrzębska
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 8. |
|
 Prosta
poprowadzona przez wierzchołki A i B trójkąta ABC utworzyła z bokiem
AC kąt 117o. Prosta prostopadła do prostej AB
przechodząca przez wierzchołek C utworzyła z bokiem BC kąt 27o.
Miara kąta CAB wynosi ......................, miara kąta ABC jest
równa ........................ . Kąt ACB ma miarę
...........................
. Prosta
poprowadzona przez wierzchołki A i B trójkąta ABC utworzyła z bokiem
AC kąt 117o. Prosta prostopadła do prostej AB
przechodząca przez wierzchołek C utworzyła z bokiem BC kąt 27o.
Miara kąta CAB wynosi ......................, miara kąta ABC jest
równa ........................ . Kąt ACB ma miarę
...........................
. |
|
Zwycięzca konkursu: Nicola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
października
wylosował:
Michał Król
uczeń:
klasy trzeciej "c"
ze
Szkoły Podstawowej
nr
29
im. Adama Mickiewicza
w
Lublinie |
|

|
|
Zadanie
nr 9. |
|
 Marta
i Zuzia w ciągu minuty nawlekły 80 koralików. Marta nawlekła cztery
razy więcej koralików niż Zuzia. Ile koralików nawlekła Marta, a ile
Zuzia? Marta
i Zuzia w ciągu minuty nawlekły 80 koralików. Marta nawlekła cztery
razy więcej koralików niż Zuzia. Ile koralików nawlekła Marta, a ile
Zuzia? |
|
Zwycięzca konkursu: Grzegorz
Węgorek
uczeń klasy: trzeciej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 10. |
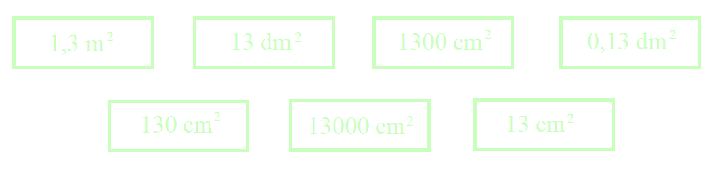
 Połącz
w pary równe pola powierzchni. Połącz
w pary równe pola powierzchni.
|
|
Zwycięzca konkursu: Agata
Pikula
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 11. |
|
 Kazik
dostał 63 orzechy, po dwóch dniach zostało 9 razy mniej. Ile
orzechów zjadł Kazik? Kazik
dostał 63 orzechy, po dwóch dniach zostało 9 razy mniej. Ile
orzechów zjadł Kazik? |
|
Zwycięzca konkursu: Katarzyna
Wróbel
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie
nr 12. |
|
 Iga
narysowała odcinek MN i zaznaczyła punkt K nienależący do prostej
MN. Następnie podzieliła odcinek MN na 7 równych części. Punkty
podziału oznaczyła kolejno A, B, C, D, E, F (punkt A znajduje się
najbliżej punktu M). Każdy z punktów na prostej połączyła z punktem
K. Wykonaj rysunek pomocniczy. Porównaj pola trójkątów MAK i EFK.
Odpowiedź uzasadnij, nie mierząc odcinków na rysunku. Iga
narysowała odcinek MN i zaznaczyła punkt K nienależący do prostej
MN. Następnie podzieliła odcinek MN na 7 równych części. Punkty
podziału oznaczyła kolejno A, B, C, D, E, F (punkt A znajduje się
najbliżej punktu M). Każdy z punktów na prostej połączyła z punktem
K. Wykonaj rysunek pomocniczy. Porównaj pola trójkątów MAK i EFK.
Odpowiedź uzasadnij, nie mierząc odcinków na rysunku. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 13. |
|
 Pięcioosobowa
rodzina wybrała się na obiad do restauracji. Wszyscy wybrali w
jednakowej cenie dania: zupę za 3 zł, a drugie danie za 8 zł i deser.
Koszt obiadu wyniósł 75 zł. Ile kosztował deser dla jednej osoby? Pięcioosobowa
rodzina wybrała się na obiad do restauracji. Wszyscy wybrali w
jednakowej cenie dania: zupę za 3 zł, a drugie danie za 8 zł i deser.
Koszt obiadu wyniósł 75 zł. Ile kosztował deser dla jednej osoby? |
|
Zwycięzca konkursu: Tymoteusz
Porębski
uczeń klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
listopada
wylosował:
Viktor Hyziak
uczeń:
klasy pierwszej "e"
z
Zespołu Szkół
nr
12
Szkoły Podstawowej
nr
14
im. Tadeusza Kościuszki
w
Lublinie |
|

|
|
Zadanie nr 14. |
|
 Ramiona
trapezu o obwodzie 70dm mają długości 17dm i 13dm, a jego wysokość
12dm. Oblicz pole tego trapezu. Wyraź je w arach. Ramiona
trapezu o obwodzie 70dm mają długości 17dm i 13dm, a jego wysokość
12dm. Oblicz pole tego trapezu. Wyraź je w arach. |
|
Zwycięzca konkursu: Tymoteusz
Porębski
uczeń klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 15. |
|
 Suma
czterech liczb wynosi 1000. Pierwszy składnik tej sumy wynosi 248, dwa
razy więcej niż drugi i o 147 mniej niż trzeci. Oblicz czwarty składnik
tej sumy. Suma
czterech liczb wynosi 1000. Pierwszy składnik tej sumy wynosi 248, dwa
razy więcej niż drugi i o 147 mniej niż trzeci. Oblicz czwarty składnik
tej sumy. |
|
Zwycięzca konkursu: Aleksandra
Lech
uczennica klasy: drugiej
"b"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 16. |
|
 W
trójkącie rozwartokątnym ABC (kat ABC jest rozwarty) |BC| = 4
cm, |AC| = 10 cm. Wysokość opuszczona z wierzchołka A ma długość 8
cm. Wykonaj rysunek pomocniczy i oblicz odległość punktu B od
prostej AC. W
trójkącie rozwartokątnym ABC (kat ABC jest rozwarty) |BC| = 4
cm, |AC| = 10 cm. Wysokość opuszczona z wierzchołka A ma długość 8
cm. Wykonaj rysunek pomocniczy i oblicz odległość punktu B od
prostej AC. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 17. |
|
 Obwód
prostokąta wynosi tyle, ile wynosi łączna długość obwodów trzech
jednakowych kwadratów o boku 3 cm. Długość tego prostokąta wynosi
tyle, ile wynosi bok kwadratu o obwodzie 48 cm. Oblicz szerokość
tego prostokąta. Obwód
prostokąta wynosi tyle, ile wynosi łączna długość obwodów trzech
jednakowych kwadratów o boku 3 cm. Długość tego prostokąta wynosi
tyle, ile wynosi bok kwadratu o obwodzie 48 cm. Oblicz szerokość
tego prostokąta. |
|
Zwycięzca konkursu: Małgorzata
Kącka
uczennica klasy: trzeciej
ze
ŹRÓDŁA -
Szkoły Podstawowej dla
Dziewcząt w
Krakowie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
grudnia
wylosowała:
Oliwia Łazińska
uczeń:
klasy pierwszej "e"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 18. |
|
 Liczba
a stanowi 4/7 wartości wyrażenia 4 .
(3,75 + 11/4 . 5) : 1/7 +
2114. Liczba b zapisana w systemie rzymskim ma postać MCDLXIV. Która
liczba a czy b jest większa i o ile? Liczba
a stanowi 4/7 wartości wyrażenia 4 .
(3,75 + 11/4 . 5) : 1/7 +
2114. Liczba b zapisana w systemie rzymskim ma postać MCDLXIV. Która
liczba a czy b jest większa i o ile? |
|
Zwycięzca konkursu: Grzegorz
Węgorek
uczeń klasy: trzeciej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 19. |
|
 Ewa
kupiła 35 cukierków. Dla siebie zostawiła 8, a resztę oddała Oli i
Julii w taki sposób, że Ola otrzymała 2 razy więcej cukierków niż
Julia. Ile cukierków dostała Ola, a ile Julia? Ewa
kupiła 35 cukierków. Dla siebie zostawiła 8, a resztę oddała Oli i
Julii w taki sposób, że Ola otrzymała 2 razy więcej cukierków niż
Julia. Ile cukierków dostała Ola, a ile Julia? |
|
Zwycięzca konkursu: Agata
Kijek
uczennica klasy: drugiej
"b"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 20. |
|
 Przeczytaj uważnie poniższy tekst. a następnie oceń prawidłowość
zapisanych pod nim zdań, wpisując w wykropkowane miejsce P, jeśli zdanie
jest prawdziwe lub F, gdy zdanie jest nieprawdziwe. Przeczytaj uważnie poniższy tekst. a następnie oceń prawidłowość
zapisanych pod nim zdań, wpisując w wykropkowane miejsce P, jeśli zdanie
jest prawdziwe lub F, gdy zdanie jest nieprawdziwe.
W sadzie pana Kowalskiego rośnie 1350 drzew. Śliwy stanowią 2/3
brzoskwiń. Czereśni jest o 50 więcej niż wiśni. Jabłoni i wiśni razem
jest 2 razy więcej niż brzoskwiń. Morele stanowią 20% wszystkich drzew.
Czereśni jest o 1/3 mniej niż moreli. Grusz jest 3 razy mniej niż
czereśni i jabłoni razem. Pozostałe drzewa to mirabelki.
a)
Liczba wiśni jest o 50 mniejsza od liczby czereśni.
.................
b) Liczba brzoskwiń jest równa połowie sumy liczby jabłoni i liczby
wiśni. .................
c) Liczba moreli jest o 1/3 większa od liczby czereśni.
.................
d) Liczba brzoskwiń jest 2,5 razy większa od liczby śliw.
................
e) Liczba wszystkich drzew oprócz moreli jest niewiele mniejsza od 1000. ................
|
|
Zwycięzca konkursu: Oliwia
Łazińska
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 21. |
|
 Joasia
zapisała numery telefonów swoich koleżanek, ale nie zanotowała przy
numerach ich imion. Pomóż jej rozwikłać tę zagadkę, jeżeli wiadomo,
że: Joasia
zapisała numery telefonów swoich koleżanek, ale nie zanotowała przy
numerach ich imion. Pomóż jej rozwikłać tę zagadkę, jeżeli wiadomo,
że:
- numer Marty zawiera trzy takie same cyfry,
- suma cyfr numeru Martyny wynosi 4,
- numer Beaty zawiera kolejne cyfry,
- numer Ani składa się
wyłącznie z cyfr, przy pomocy których zapisujemy
liczby
parzyste.
Połącz imiona dziewczynek z odpowiednimi numerami telefonów.
|
MARTA |
8 6 2 4 2 8 |
|
|
MARTYNA |
1 2 3 4 5 6
|
|
|
BEATA |
4 9 6 0 0 0
|
|
|
ANIA |
5 7 3 8 0 1 |
|
|
KLAUDIA
|
1 0 1 2 0 0
|
|
|
|
Zwycięzca konkursu: Olga
Jabłońska
uczennica klasy: pierwszej
"e"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
stycznia
wylosował:
Miłosz Wroński
uczeń:
klasy pierwszej "a"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 22. |
|
 Mama
zebrała 12,2 kg nasion i zapakowała je do różnych woreczków,
wypełniając je w całości. Do woreczków, które wykorzystała można
było wsypać odpowiednio: 0,3 kg, 0,33 kg i 0,65 kg nasion.
Największych woreczków było o 6 mniej niż najmniejszych. Woreczków,
do których zapakowała po o,33 kg nasion było 2 razy więcej niż
najmniejszych. Oblicz, ile mama napełniła największych woreczków. Mama
zebrała 12,2 kg nasion i zapakowała je do różnych woreczków,
wypełniając je w całości. Do woreczków, które wykorzystała można
było wsypać odpowiednio: 0,3 kg, 0,33 kg i 0,65 kg nasion.
Największych woreczków było o 6 mniej niż najmniejszych. Woreczków,
do których zapakowała po o,33 kg nasion było 2 razy więcej niż
najmniejszych. Oblicz, ile mama napełniła największych woreczków. |
|
Zwycięzca konkursu: Filip
Tolarz
uczeń klasy: trzeciej
z
Zespołu Szkolno-Przedszkolnego nr
1,
Szkoły Podstawowej nr
16 im.
Adama Dzika w
Wodzisławiu Śląskim
|
|
Zadanie nr 23. |
|
 Poniższe
liczby zostały zapisane zgodnie z pewną regułą. Odkryj ją i dopisz
cztery następne liczby. Poniższe
liczby zostały zapisane zgodnie z pewną regułą. Odkryj ją i dopisz
cztery następne liczby.
a)
9, 18, 27, 36, 45,
.........................................................
b)
3, 18, 33, 48, 63,
.........................................................
c)
1, 2, 4, 7, 11, 16, 22,
................................................... |
|
Zwycięzca konkursu: Igor
Wieczorkiewicz
uczeń klasy: pierwszej
"e"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 24. |
|
 Zosia
napisała pewną liczbę. Marysia napisała liczbę pięć razy większą niż
Zosia. Obie dziewczynki podzieliły swoje liczby przez 9. Zosia
otrzymała resztę 7, Marysia otrzymała resztę ... . Zosia
napisała pewną liczbę. Marysia napisała liczbę pięć razy większą niż
Zosia. Obie dziewczynki podzieliły swoje liczby przez 9. Zosia
otrzymała resztę 7, Marysia otrzymała resztę ... . |
|
Zwycięzca konkursu: Natalia
Ruda
uczennica klasy: pierwszej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 25. |
|
 Krzyś
okrąża stadion przez 2 minuty, a Robert przez 3 minuty. Po ilu
minutach od startu obaj równocześnie przebiegną linię mety? Krzyś
okrąża stadion przez 2 minuty, a Robert przez 3 minuty. Po ilu
minutach od startu obaj równocześnie przebiegną linię mety? |
|
Zwycięzca konkursu: Natalia
Pachała
uczennica klasy: pierwszej
"g"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 26. |
|
 Ania
zaznaczyła na osi liczbowej punkty A, B, C, D, E odpowiadające
odpowiednio liczbom: Ania
zaznaczyła na osi liczbowej punkty A, B, C, D, E odpowiadające
odpowiednio liczbom:
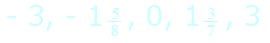
Najmniejszą długość ma odcinek ..............., wynosi ona
........................ .
|
|
Zwycięzca konkursu: Natalia
Ruda
uczennica klasy: pierwszej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
lutego
wylosowała:
Zofia Mielnik
uczennica:
klasy pierwszej "b"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 27. |
|
 Monika
ma 12 lat, tata jest cztery razy starszy. Ile lat będzie miała
Monika w pięćdziesiąte urodziny taty? Monika
ma 12 lat, tata jest cztery razy starszy. Ile lat będzie miała
Monika w pięćdziesiąte urodziny taty? |
|
Zwycięzca konkursu: Natalia
Piwoni
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 28. |
|
 W
piątek klasa VIa pisała sprawdzian z matematyki. Janek był
chory, więc nie przystąpił do sprawdzianu. Najniższą oceną z tego
sprawdzianu była trójka. Żaden uczeń nie otrzymał szóstki. Połowa
piszących otrzymała oceny dobre, co trzeci uczeń otrzymał piątkę, a
tylko czterech uczniów otrzymało ocenę dostateczną. Ta klasa liczy
... uczniów. Ocenę bardzo dobrą z tego sprawdzianu otrzymało ...
uczniów. Oceny dostateczne stanowiły ...% ocen dobrych. W
piątek klasa VIa pisała sprawdzian z matematyki. Janek był
chory, więc nie przystąpił do sprawdzianu. Najniższą oceną z tego
sprawdzianu była trójka. Żaden uczeń nie otrzymał szóstki. Połowa
piszących otrzymała oceny dobre, co trzeci uczeń otrzymał piątkę, a
tylko czterech uczniów otrzymało ocenę dostateczną. Ta klasa liczy
... uczniów. Ocenę bardzo dobrą z tego sprawdzianu otrzymało ...
uczniów. Oceny dostateczne stanowiły ...% ocen dobrych. |
|
Zwycięzca konkursu: Tymon
Kosiarski
uczeń klasy: pierwszej
"e"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
Zadanie nr 29. |
|
 Suma
trzech liczb jest równa 82. Pierwszy składnik jest o 5 większy od
drugiego, trzeci natomiast 5 razy większy od drugiego składnika.
Jakie to liczby? Suma
trzech liczb jest równa 82. Pierwszy składnik jest o 5 większy od
drugiego, trzeci natomiast 5 razy większy od drugiego składnika.
Jakie to liczby? |
|
Zwycięzca konkursu: Jakub
Stanikowski
uczeń klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 30. |
|
 Hania
zbiera znaczki. 25% kolekcji stanowią znaczki polskie. Wśród
znaczków zagranicznych Hania ma znaczki państw europejskich oraz 15
znaczków amerykańskich. Znaczki europejskie stanowią 80% znaczków
zagranicznych. Hania ma ............... znaczków polskich. Znaczków
europejskich ma .............. razy więcej niż polskich. Znaczków
zagranicznych ma o .................. więcej niż polskich. Kolekcja
Hani liczy ............. znaczków. Hania
zbiera znaczki. 25% kolekcji stanowią znaczki polskie. Wśród
znaczków zagranicznych Hania ma znaczki państw europejskich oraz 15
znaczków amerykańskich. Znaczki europejskie stanowią 80% znaczków
zagranicznych. Hania ma ............... znaczków polskich. Znaczków
europejskich ma .............. razy więcej niż polskich. Znaczków
zagranicznych ma o .................. więcej niż polskich. Kolekcja
Hani liczy ............. znaczków. |
|
Zwycięzca konkursu: Lena
Dejnek
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
marca
wylosowała:
Maja Gawda
uczennica:
klasy pierwszej "a"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 31. |
|
 W
misce jest 8 śliwek. Jabłek i gruszek jest trzy razy więcej niż
śliwek. Jabłek jest o 10 mniej niż gruszek. Ile jest jabłek, a ile
gruszek? Ile owoców jest w misce? W
misce jest 8 śliwek. Jabłek i gruszek jest trzy razy więcej niż
śliwek. Jabłek jest o 10 mniej niż gruszek. Ile jest jabłek, a ile
gruszek? Ile owoców jest w misce? |
|
Zwycięzca konkursu: Kamila
Wikieta
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 32. |
 Basia
się urodziła w styczniu 2014 r.. Jej mama miała wtedy 27 lat. Basia
się urodziła w styczniu 2014 r.. Jej mama miała wtedy 27 lat.
a) Mama będzie cztery razy starsza od Basi za ..... lat.
Wówczas razem będą miały .....
lat.
b) Wiek Basi będzie stanowił 0,4 wieku mamy, gdy Basia będzie
obchodziła swoje .......
urodziny. Wówczas wspólne dzielniki
liczb oznaczających wiek każdej
z nich
napisane w kolejności rosnącej (bez przecinków) utworzą
liczbę ........ .
|
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 33. |
|
 Co
to za liczba, która składa się z trzech setek i dwóch dziesiątek? a)
Podaj liczbę o 400 większą od tej liczby. b) Podaj liczbę 2 razy
mniejszą od tej liczby. c) Podaj liczbę mniejszą od niej o 120. d) Podaj
liczbę 3 razy większą od tej liczby. Co
to za liczba, która składa się z trzech setek i dwóch dziesiątek? a)
Podaj liczbę o 400 większą od tej liczby. b) Podaj liczbę 2 razy
mniejszą od tej liczby. c) Podaj liczbę mniejszą od niej o 120. d) Podaj
liczbę 3 razy większą od tej liczby. |
|
Zwycięzca konkursu: Natalia
Piwoni
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 34. |
|
 Zapisz
w postaci wyrażenia różnicę podwojonego sześcianu liczby x i
kwadratu podwojonej liczby x. Zapisz
w postaci wyrażenia różnicę podwojonego sześcianu liczby x i
kwadratu podwojonej liczby x. |
|
Zwycięzca konkursu: Kamila
Wikieta
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
kwietnia
wylosował:
Grzegorz Zubilewicz
uczennica:
klasy trzeciej "a"
z
Zespołu Szkół
nr
8
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 35. |
|
 Jaką
odległość pokona w ciągu czterech godzin samochód jadący z
prędkością 65 km/h ? Jaką
odległość pokona w ciągu czterech godzin samochód jadący z
prędkością 65 km/h ? |
|
Zwycięzca konkursu: Wojciech
Kucia
uczeń klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 36. |
 Oceń
prawdziwość poniższych zdań, wpisując w wykropkowane miejsce P,
jeśli zdanie jest prawdziwe lub F, gdy zdanie jest nieprawdziwe. Oceń
prawdziwość poniższych zdań, wpisując w wykropkowane miejsce P,
jeśli zdanie jest prawdziwe lub F, gdy zdanie jest nieprawdziwe.
a) Każda cięciwa okręgu o promieniu długości 5 cm ma długość
mniejszą od 10 cm. .....
b) Istnieje trójkąt, który nie ma osi symetrii. .....
c) Objętość graniastosłupa o podstawie trójkąta i wysokości H jest
równa objętości
ostrosłupa o podstawie takiego samego trójkąta i wysokości H.
.....
d) Trójkąt, w którym jeden z kątów ma miarę równą średniej
arytmetycznej miar
wszystkich trzech kątów jest trójkątem
równobocznym. .... |
|
Zwycięzca konkursu: Anna
Domańska
uczennica klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 37. |
|
 Cztery
czekolady podzielono po równo na troje dzieci. Jaką część otrzyma
każde dziecko? Cztery
czekolady podzielono po równo na troje dzieci. Jaką część otrzyma
każde dziecko? |
|
Zwycięzca konkursu: Michał
Zarych
uczeń klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 38. |
|
 Każdy
bok prostokątnego placu o obwodzie 190 m obsadzono drzewkami w taki
sposób, że w każdym wierzchołku rośnie jedno drzewko. Wzdłuż
krótszego boku posadzono 15 drzewek, wzdłuż dłuższego 21.
Przyjmujemy, że drzewka rosnące w wierzchołkach nie należą do
żadnego boku prostokąta. Odległości miedzy drzewkami są równe. Jedno
drzewko rośnie od drugiego w odległości ..... m. Krótszy bok
prostokąta ma długość ..... m. Ten plac ma powierzchnię równą .....
m2, czyli .....ha. Każdy
bok prostokątnego placu o obwodzie 190 m obsadzono drzewkami w taki
sposób, że w każdym wierzchołku rośnie jedno drzewko. Wzdłuż
krótszego boku posadzono 15 drzewek, wzdłuż dłuższego 21.
Przyjmujemy, że drzewka rosnące w wierzchołkach nie należą do
żadnego boku prostokąta. Odległości miedzy drzewkami są równe. Jedno
drzewko rośnie od drugiego w odległości ..... m. Krótszy bok
prostokąta ma długość ..... m. Ten plac ma powierzchnię równą .....
m2, czyli .....ha. |
|
Zwycięzca konkursu: Filip
Małek
uczeń klasy: pierwszej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 39. |
|
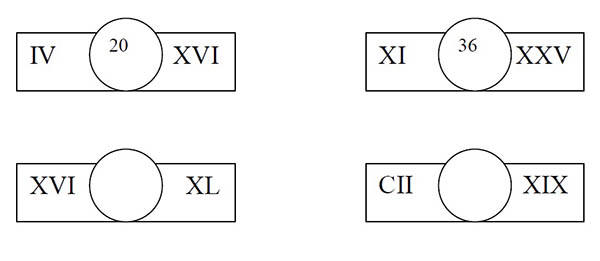
 Liczby
w kółkach zostały zapisane według pewnej reguły. Odkryj ją i wpisz
odpowiednie liczby w wolne miejsca. Liczby
w kółkach zostały zapisane według pewnej reguły. Odkryj ją i wpisz
odpowiednie liczby w wolne miejsca.
|
|
Zwycięzca konkursu: Mateusz
Dejnek
uczeń klasy: drugiej
"b"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
maja
wylosował:
Szymon Skałecki
uczennica:
klasy drugiej "b"
z
Zespołu Szkół
nr
12,
Szkoły Podstawowej
nr
14
im. Tadeusza Kościuszki
w
Lublinie |
|

|
|
Zadanie nr 40. |
|
 Jaś
nasypał 18000 cm3 piasku do prostopadłościennego pudełka o podstawie
kwadratu o boku długości 0,6 m. Piasek wypełnił pudełko do 0,4
wysokości. Wysokość tego pudełka wynosi ...... dm. Na oklejenie
ścian bocznych tego pudełka potrzeba ....... dm2 papieru. Jaś ma
zeszyt papierów kolorowych zawierający 10 kartek o wymiarach 19 cm i
11 cm każda. Do oklejenia ścian bocznych tego pudełka zabraknie mu
....... całych kartek papieru kolorowego. Jaś
nasypał 18000 cm3 piasku do prostopadłościennego pudełka o podstawie
kwadratu o boku długości 0,6 m. Piasek wypełnił pudełko do 0,4
wysokości. Wysokość tego pudełka wynosi ...... dm. Na oklejenie
ścian bocznych tego pudełka potrzeba ....... dm2 papieru. Jaś ma
zeszyt papierów kolorowych zawierający 10 kartek o wymiarach 19 cm i
11 cm każda. Do oklejenia ścian bocznych tego pudełka zabraknie mu
....... całych kartek papieru kolorowego. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 41. |
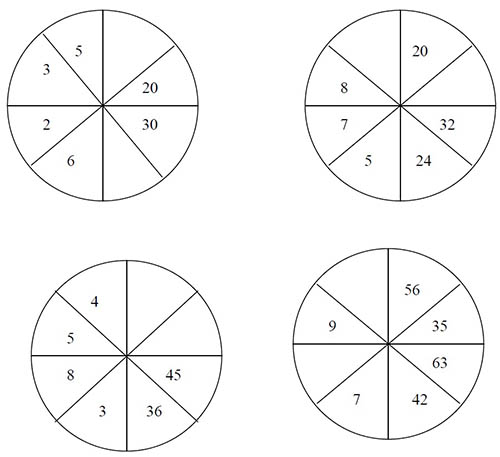
 Liczby
wpisano w koła według pewnych reguł. Uzupełnij puste pola. Liczby
wpisano w koła według pewnych reguł. Uzupełnij puste pola.
|
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 42. |
|
 W
sześcianie ABCDEFGH środek podstawy EFGH oznaczono literą K i
połączono z wierzchołkami A i B. Wykonaj rysunek i oblicz pole
trójkąta ABK wiedząc, że krawędź sześcianu ma długość 6 cm. W
sześcianie ABCDEFGH środek podstawy EFGH oznaczono literą K i
połączono z wierzchołkami A i B. Wykonaj rysunek i oblicz pole
trójkąta ABK wiedząc, że krawędź sześcianu ma długość 6 cm. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 43. |
|
 Babcia
upiekła rogaliki. Policzyła je i zastanowiła się, po ile rogalików dać
każdemu wnukowi: „Jeżeli dam każdemu po 5, to zabraknie mi 3 rogalików.
Jeżeli dam każdemu po 4, to zostaną mi 3. Ile wnuków miała babcia? Babcia
upiekła rogaliki. Policzyła je i zastanowiła się, po ile rogalików dać
każdemu wnukowi: „Jeżeli dam każdemu po 5, to zabraknie mi 3 rogalików.
Jeżeli dam każdemu po 4, to zostaną mi 3. Ile wnuków miała babcia? |
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
Uwaga!:
nagrodę-niespodziankę
miesiąca
czerwca
wylosowała:
Nikola Adamczyk
uczennica:
klasy drugiej "a"
z
Zespołu Szkół
nr
8,
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 44. |
|
 Prostokąt
i kwadrat mają równe obwody. W prostokącie jeden bok jest 2 razy dłuższy
od drugiego. Oblicz, jaką częścią pola kwadratu jest pole prostokąta.
Wynik zapisz w najprostszej postaci. Uwaga! Zadanie rozwiąż nie podając
przykładowych wartości liczbowych długości boków prostokąta i kwadratu. Prostokąt
i kwadrat mają równe obwody. W prostokącie jeden bok jest 2 razy dłuższy
od drugiego. Oblicz, jaką częścią pola kwadratu jest pole prostokąta.
Wynik zapisz w najprostszej postaci. Uwaga! Zadanie rozwiąż nie podając
przykładowych wartości liczbowych długości boków prostokąta i kwadratu. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 45. |
 Napisz
treść zadania do działania: Napisz
treść zadania do działania:
20 + (20 + 3) + 20 : 2 = |
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 46. |
|
 Na
uszycie pewnej spódnicy zużyto 0,8 m materiału. Dodatki, czyli zamek,
nici i guzik, stanowiły 15% wartości materiału, z którego uszyto
spódnicę. Koszty wykonania, podatek oraz marża sklepu prowadzącego
sprzedaż powiększyły wartość tej spódnicy o 48 zł. Pani Kowalska kupiła
w kwietniu taką spódnicę za 94 zł. Oblicz, ile trzeba będzie zapłacić za
taką spódnicę w tym sklepie w czerwcu wiedząc, że cena materiału wzrosła
o 20%, a inne koszty nie uległy zmianie. Na
uszycie pewnej spódnicy zużyto 0,8 m materiału. Dodatki, czyli zamek,
nici i guzik, stanowiły 15% wartości materiału, z którego uszyto
spódnicę. Koszty wykonania, podatek oraz marża sklepu prowadzącego
sprzedaż powiększyły wartość tej spódnicy o 48 zł. Pani Kowalska kupiła
w kwietniu taką spódnicę za 94 zł. Oblicz, ile trzeba będzie zapłacić za
taką spódnicę w tym sklepie w czerwcu wiedząc, że cena materiału wzrosła
o 20%, a inne koszty nie uległy zmianie. |
|
Zwycięzca konkursu: Brak
nadesłanych rozwiązań |
|
Zadanie nr 47. |
|
 W
trzech klasach trzecich jest 85 uczniów. W kl. III a i III b jest 59
uczniów, a w klasie III b i III c - 56 uczniów. Ilu uczniów jest w
każdej klasie trzeciej? W
trzech klasach trzecich jest 85 uczniów. W kl. III a i III b jest 59
uczniów, a w klasie III b i III c - 56 uczniów. Ilu uczniów jest w
każdej klasie trzeciej? |
|
Zwycięzca konkursu: Tymoteusz
Porębski
uczeń klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|

|
|
 Uwaga!:
nagrodę-niespodziankę
miesiąca
lipca
Uwaga!:
nagrodę-niespodziankę
miesiąca
lipca
wylosowała:
Nikola Adamczyk
uczennica:
klasy drugiej "a"
z
Zespołu Szkół
nr
8,
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
Zadanie nr 48. |
|
 Basia
ma trzy siostry, a każda z jej sióstr ma dwóch braci. Ile dzieci
jest w tej rodzinie? Basia
ma trzy siostry, a każda z jej sióstr ma dwóch braci. Ile dzieci
jest w tej rodzinie? |
|
Zwycięzca konkursu: Tymoteusz
Porębski
uczeń klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 49. |
|
 W
sali gimnastycznej ustawiono 80 krzeseł zielonych i żółtych. Krzesła
żółte stały w ośmiu rzędach po 8 sztuk w każdym rzędzie. Krzesła zielone
ustawiono na scenie. Ile jest zielonych krzeseł? W
sali gimnastycznej ustawiono 80 krzeseł zielonych i żółtych. Krzesła
żółte stały w ośmiu rzędach po 8 sztuk w każdym rzędzie. Krzesła zielone
ustawiono na scenie. Ile jest zielonych krzeseł?
Rozwiąż to
równanie, które jest rozwiązaniem zadania.
8 . x + 8 = 80
80 + x = 8 . 8
x + 8 . 8 = 80 |
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 50. |
 Ile
jest takich miesięcy w roku, które są dłuższe niż cztery i pół tygodnia? Ile
jest takich miesięcy w roku, które są dłuższe niż cztery i pół tygodnia? |
|
Zwycięzca konkursu: Nikola
Adamczyk
uczennica klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 51. |
 Narysuj
kwadrat, który składa się z 144 kratek. Narysuj
kwadrat, który składa się z 144 kratek. |
|
Zwycięzca konkursu: Tymoteusz
Porębski
uczeń klasy: drugiej
"a"
z
Zespołu Szkół nr
8,
Szkoły Podstawowej nr
39 im.
Szarych Szeregów w
Lublinie
|
|
Zadanie nr 52. |
|
 Pewien
miesiąc trwał równo cztery tygodnie. Ile dni miał następujący po nim
miesiąc? Pewien
miesiąc trwał równo cztery tygodnie. Ile dni miał następujący po nim
miesiąc? |
|
Zwycięzca konkursu: Agata
Kijek
uczennica klasy: drugiej
"b"
z
Zespołu Szkół nr
12,
Szkoły Podstawowej nr
14 im.
Tadeusza Kościuszki w
Lublinie
|
|
|

|
|
 Uwaga!:
nagrodę-niespodziankę
miesiąca
sierpnia
Uwaga!:
nagrodę-niespodziankę
miesiąca
sierpnia
wylosowała:
Oliwia Łazińska
uczennica:
klasy drugiej "a"
z
Zespołu Szkół
nr
8,
Szkoły Podstawowej
nr
39
im. Szarych Szeregów
w
Lublinie |
|

|
|
|
|
 Nagrodę roku szkolnego
2018/2019 Nagrodę roku szkolnego
2018/2019
wylosowała:
Małgorzata Kącka
uczennica:
klasy trzeciej
ze
Szkoły Podstawowej dla Dziewcząt "ŹRÓDŁO"
w Krakowie-Azory
|
|

|
|
|

Gratulujemy
Zwycięzcom
i zapraszamy
do udziału w konkursie
"Zadań tygodnia"
w Nowym Roku Szkolnym 2019/2020.

|
|
|

 Powrót na stronę główną
Powrót na stronę główną |
 Rozwiąż
rebus:
Rozwiąż
rebus: Połącz
w pary równe pola powierzchni.
Połącz
w pary równe pola powierzchni. Basia
się urodziła w styczniu 2014 r.. Jej mama miała wtedy 27 lat.
Basia
się urodziła w styczniu 2014 r.. Jej mama miała wtedy 27 lat. Oceń
prawdziwość poniższych zdań, wpisując w wykropkowane miejsce P,
jeśli zdanie jest prawdziwe lub F, gdy zdanie jest nieprawdziwe.
Oceń
prawdziwość poniższych zdań, wpisując w wykropkowane miejsce P,
jeśli zdanie jest prawdziwe lub F, gdy zdanie jest nieprawdziwe. Liczby
wpisano w koła według pewnych reguł. Uzupełnij puste pola.
Liczby
wpisano w koła według pewnych reguł. Uzupełnij puste pola. Napisz
treść zadania do działania:
Napisz
treść zadania do działania: Ile
jest takich miesięcy w roku, które są dłuższe niż cztery i pół tygodnia?
Ile
jest takich miesięcy w roku, które są dłuższe niż cztery i pół tygodnia? Narysuj
kwadrat, który składa się z 144 kratek.
Narysuj
kwadrat, który składa się z 144 kratek. 




