Archiwum  zadań  tygodnia 2015-2016

  Zadania tygodnia - 2014/2015
  Zadania tygodnia - 2015/2016
  Zadania tygodnia - 2016/2017
  Zadania tygodnia - 2017/2018
  Zadania tygodnia - 2018/2019
  Zadania tygodnia - 2019/2020
  Zadania tygodnia - 2020/2021
  Zadania tygodnia - 2021/2022
  Zadania tygodnia - 2022/2023
  Zadania tygodnia - 2023/2024

Zadania tygodnia kierowane są do wszystkich zainteresowanych uczniów kl. I-III  szkół podstawowych.
 

  Suma trzech kolejnych dwucyfrowych liczb parzystych jest równa 42. Znajdź te liczby.

Zwycięzca konkursu: Laura Ziemecka
uczennica: klasy drugiej "c"
z Zespołu Szkół nr 12 , Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

  Pociąg o długości 200 m jedzie przez tunel o długości 200 m z prędkością 200 km/h. Ile czasu potrzebuje on na pokonanie tego tunelu?

Zwycięzca konkursu: Kacper Sapalski
uczeń: klasy pierwszej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Zwycięzca konkursu: Kacper Próchniak
uczeń: klasy pierwszej "c"
z Zespołu Szkół nr 12 , Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

  Ile jest kwadratów na tym rysunku? 

                  Uwaga: każdy najmniejszy element figury jest kwadratem.

Zwycięzca konkursu: Karolina Korkosz
uczennica: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca września
wylosowała: Oliwia Łukaszek
uczennica: klasy pierwszej "b"
z  Zespołu Szkół nr 8,  Szkoły Podstawowej  nr 39  im. Aleksandra Kamińskiego  w  Lublinie.

  Podłoga w pokoju Marcela ma kształt kwadratu o obwodzie równym 20 m, na jej środku leży kwadratowy dywan oddalony od każdej ściany pokoju o 1 m. Oblicz, długość obwodu tego dywanu.

Zwycięzca konkursu: Mateusz Wieczorek
uczeń: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Zegarek elektroniczny (cyfrowy) śpieszy się 5 minut 36 sekund na tydzień. Jeśli w niedzielę w południe pokazuje on dokładny czas, to jaki czas pokaże w następny piątek o piątej po południu?

Zwycięzca konkursu: Szymon Mendel
uczeń: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Marcel przechowuje kolekcję swoich 41 monet w trzech albumach. W pierwszym albumie jest dwa razy mniej monet niż w drugim, a w trzecim albumie jest o 7 monet mniej niż w pierwszym. Oblicz, ile monet jest w każdym albumie.

Zwycięzca konkursu: Jan Chorągiewicz
uczeń: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Suma dwóch liczb naturalnych jest równa 47. Dzieląc większą z nich przez mniejszą otrzymujesz iloraz 2 i resztę 5. Jaka jest wartość większej z tych liczb?

Zwycięzca konkursu: Jakub Matela
uczeń: klasy pierwszej "f"
z Zespołu Szkół nr 12 , Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca października
wylosował: Adam Krawczyk
uczeń: klasy trzeciej "c"
ze Szkoły Podstawowej  nr 29  im. Adama Mickiewicza  w  Lublinie.

Zadanie nr 9.

  Marcel przechowuje kolekcję swoich 43 monet w trzech albumach. W drugim albumie jest dwa razy więcej monet niż w pierwszym, a w trzecim albumie jest o 7 monet więcej niż w pierwszym. Oblicz, ile monet jest w każdym albumie.

Zwycięzca konkursu: Antoni Dybała
uczeń: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Na planie w skali 1 : 2500 pewien teren ma kształt prostokąta o wymiarach 64 mm długości i 48 mm szerokości. Jaka jest prawdziwa powierzchnia tego terenu?

                                                                                               64 mm

                                                                     
                                                                      48 mm

Zwycięzca konkursu: Patryk Zielonka
uczeń: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Na przygotowanie ogrodzenia prostokątnej działki potrzeba tyle samo siatki, co na ogrodzenie dwóch działek kwadratowych: jedna o boku 9 metrów, a druga o boku 11 metrów. Szerokość tej działki jest równa długości boku trójkąta równobocznego o obwodzie 36 metrów. Oblicz, jaką długość ma dłuższy bok tej działki.

Zwycięzca konkursu: Dominika Gil
uczennica: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Z pnia arytmokaliptusa wyrastają trzy potężne konary. Z każdego z nich wyrastają cztery gałęzie, z każdej z nich po sześć mniejszych gałęzi, z tych zaś po osiem małych gałązek. Na końcu każdej z nich rosną po dwa kwiaty malwy. Ile kwiatów posiada arytmokaliptus?

Zwycięzca konkursu: Stanisław Karapuda
uczeń: klasy trzeciej "d"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca listopada
wylosowała: Julia Galus
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej  nr 29  im. Adama Mickiewicza  w  Lublinie.

  Na przygotowanie ogrodzenia prostokątnej działki potrzeba tyle samo siatki, co na ogrodzenie działki kwadratowej o boku 15 metrów. Szerokość tej działki jest równa długości boku trójkąta równobocznego o obwodzie 27 metrów. Oblicz, jaką długość ma dłuższy bok tej działki.

Zwycięzca konkursu: Bianka Kuś
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Zając biegnie 35 razy szybciej niż żółw, który na przebycie trasy wyścigu potrzebuje 2 h 20 min. Z jakim wyprzedzeniem wystartować musi żółw, aby obaj przyjaciele przybiegli do mety razem?

Zwycięzca konkursu: Tomasz Serewa
uczeń: klasy pierwszej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Zwycięzca konkursu: Wiktoria Oryszczuk
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Do sporządzenia ogromnego omletu użyto 6 tuzinów wytłaczanek zawierających po tuzinie jaj każda? Z ilu jaj zrobiono ten omlet?

Zwycięzca konkursu: Katarzyna Charko
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

Zwycięzca konkursu: Karol Podleśny
uczeń: klasy pierwszej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca grudnia
wylosował: Aleksander Pyzik
uczeń: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Wczoraj było 12,5% nieobecnych w klasie. Dziś nieobecny jest dodatkowo 1 uczeń. Ilość obecnych jest dziś 5 razy większa niż ilość nieobecnych. Ilu uczniów liczy ta klasa?

Zwycięzca konkursu: Wiktoria Kulik
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 12, Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

Zwycięzca konkursu: Szymon Szewczyk
uczeń: klasy trzeciej "a"
ze Szkoły Podstawowej nr 40 im. Leona Kruczkowskiego w Lublinie

Zwycięzca konkursu: Jadwiga Myna
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Kopa to 60 sztuk, mendel jest 4 razy mniejszy od kopy i o 3 większy od tuzina. Oblicz, ile tuzinów, a ile mendli mieści się w dwóch kopach.
 

Zwycięzca konkursu: Krzysztof Oleszczuk
uczeń: klasy drugiej "f"
z Zespołu Szkół nr 12, Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca stycznia
wylosował: Kacper Szulc
uczeń: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  W spiżarni babci znajduje się słoik zawierający 650 g dżemu. Wnuczek Tomek wyjada z niego codziennie 5 łyżeczek dżemu. Każda łyżeczka zawiera 6 g dżemu. Ile dżemu zostanie w słoiku po 20 dniach?

Zwycięzca konkursu: Nikola Smagło
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Przez 3 dzielą się liczby, których suma cyfr jest podzielna przez 3, przez 4 dzielą się liczby, których cyfra dziesiątek i cyfra jedności tworzą liczbę podzielną przez 4. W miejsce kropek wstaw cyfrę, tak by powstała liczba była podzielna i przez 3 i przez 4.

13...

Zwycięzca konkursu: Kaja Możdżeń
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Należy pomalować wszystkie ściany sześcianu. Suma długości wszystkich krawędzi wynosi 2,16 m. Na pomalowanie 1 m2 powierzchni potrzeba 1 kg farby. Ile farby potrzeba na pomalowanie wszystkich ścian sześcianu?

Zwycięzca konkursu: Radosław Sołtys
uczeń: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Karol zapisał 4 liczby tak, że druga liczba jest o 6 większa od pierwszej, trzecia liczba jest o 12 większa od drugiej, a czwarta liczba jest o 24 większa od trzeciej. Jakie to liczby, jeśli suma wszystkich zapisanych liczb jest równa 78?

Zwycięzca konkursu: Amelia Wójtowicz
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca lutego
wylosowała: Natalia Czmuda
uczennica: klasy trzeciej "c"
z Zespołu Szkół nr 12, Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

  Suma długości wszystkich krawędzi prostopadłościanu wynosi 108 cm. Długości dwóch krawędzi prostopadłościanu wychodzących z tego samego wierzchołka wynoszą odpowiednio: 12 cm i 8 cm. Jaką długość ma trzecia krawędź wychodząca z tego samego wierzchołka?

Zwycięzca konkursu: Adam Chojnacki
uczeń: klasy pierwszej "c"
z Zespołu Szkół nr 12, Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

  Karol zapisał 4 liczby tak, że druga liczba jest o 6 większa od pierwszej, trzecia liczba jest o 12 większa od pierwszej, a czwarta liczba jest o 24 większa od pierwszej. Jakie to liczby, jeśli suma wszystkich zapisanych liczb jest równa 58?

Zwycięzca konkursu: Mateusz Smyk
uczeń: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Jaka to liczba, która ma następującą własność: jeśli dodamy do niej jej połowę, to otrzymamy liczbę o 3 mniejszą od jej dwukrotności?

Zwycięzca konkursu: Julia Tuziemska
uczennica: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Karol miał kilkanaście cukierków, połowę z nich oddał młodszej siostrze, połowę z tego co mu zostało oddał bratu, a połowę z tego co mu jeszcze zostało oddał koledze. Oblicz, ile cukierków miał Karol na początku, jeśli po wszystkich operacjach zostały mu dwa cukierki.

Zwycięzca konkursu: Agata Krzewińska
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca marca
wylosował: Mateusz Smyk
uczeń: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Wałbrzych - Plac Magistracki z Ratuszem

Lata 103- 905

Zwycięzca konkursu: Sada Habieb
uczennica: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Babcia przygotowała 8 litrów soku z czarnej porzeczki i tyle samo soku z truskawek. Przygotowany sok chce rozlać do 9 słoików półlitrowych, a resztę do butelek. Litr soku mieści się w 4 takich butelkach. Oblicz, ile butelek musi przygotować babcia, aby rozlać cały sok.

Zwycięzca konkursu: Bartłomiej Muca
uczeń: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Źródło wody o wydajności 80 litrów na minutę zasila dwie fontanny, z których jedna pobiera 4 razy więcej wody niż druga. Ile wody w ciągu minuty pobiera ta, która pobiera jej więcej?

Zwycięzca konkursu: Natalia Kusiak
uczeń: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Marcin ma w trzech przegródkach karty z piłkarzami. W pierwszej i trzeciej przegródce ma razem 13 kart, w drugiej i trzeciej 15, a w pierwszej i drugiej 12. Oblicz, ile kart ma Marcin w każdej przegródce.

Zwycięzca konkursu: Jadwiga Myna
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Mam w kieszeni 51 banknotów wyłącznie stu- i dwudziesto- złotowych. Wiedząc, że mam w sumie 3500 zł, ile mam banknotów stuzłotowych?

Zwycięzca konkursu: Oliwia Łukaszek
uczennica: klasy pierwszej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca kwietnia
wylosował: Filip Michoń
uczeń: klasy drugiej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

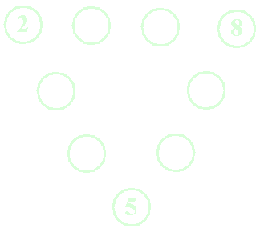
  Mając do dyspozycji liczby od 1 - 9 wpisz je w koła tak, aby powstał trójkąt magiczny (suma liczb na wszystkich bokach trójkąta jest taka sama), trzy liczby są już wpisane.

Zwycięzca konkursu: Szymon Mendel
uczeń: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

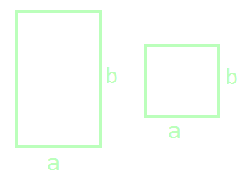
  Jeśli zmniejszymy o 7 cm długość prostokąta otrzymamy kwadrat o obwodzie 32 cm. Jaka była początkowa szerokość prostokąta?

Zwycięzca konkursu: Natalia Czmuda
uczennica: klasy trzeciej "c"
z Zespołu Szkół nr 12, Szkoły Podstawowej nr 14 im. Tadeusza Kościuszki w Lublinie

  Kacper za 4 lata będzie miał tyle samo lat co jego siostra Tamara ma w tej chwili. 3 lata temu oboje mieli łącznie 14 lat. Oblicz obecny wiek Kacpra i Tamary.

Zwycięzca konkursu: Nikola Smagło
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Zwycięzca konkursu: Katarzyna Charko
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Tadzio stanął w kolejce do okienka stołówki. Policzył, że w kolejce jest razem 19 dzieci i za nim znajduje się 5 razy więcej dzieci niż przed nim. Oblicz, którym z kolei dzieckiem w tej kolejce jest Tadzio?

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca maja
wylosował: Bartłomiej Muca
uczeń: klasy drugiej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Ela przyszła na przyjęcie urodzinowe Ani 5 minut wcześniej niż Staś, lecz 2 minuty później niż Iwona. Iwona pierwsza opuściła przyjęcie. Wyszła 2 minuty wcześniej niż Staś i 5 minut wcześniej niż Ela. Ile minut dłużej od Stasia przebywała na przyjęciu Ela?

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Kasia obliczyła, że w czasie przyrządzania jednej porcji kiełbasy na gorąco mama gotuje ją przez 5 minut. Mama Kasi właśnie wrzuca do garnka z gotującą się wodą trzy porcje kiełbasy. Oblicz, ile czasu zajmie jej gotowanie.

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Królewna Śnieżka ustawiła 7 krasnoludków wg wzrostu od najniższego do najwyższego i rozdzieliła pomiędzy nich 77 jagód zebranych przez nich w lesie. Najniższy krasnal otrzymał pewną porcję jagód, a każdy następny w kolejce otrzymał o jedną jagodę więcej niż jego poprzednik. Ile jagód otrzymał najwyższy krasnoludek?

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  W trzech pojemnikach znajduje się 79 piłek. Gdy z pierwszego pojemnika wyjmiemy 1 piłkę, z drugiego 12, a do trzeciego pojemnika dołożymy 6 piłek z tych co wyjęliśmy z poprzednich, w każdym pojemniku będzie ich po tyle samo. Oblicz, ile piłek jest w każdym pojemniku.

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Uwaga!: nagrodę-niespodziankę miesiąca czerwca
wylosowała: Jadwiga Myna
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  W wesołym miasteczku ceny biletów na cztery rodzaje karuzel wynoszą odpowiednio 2 zł, 3 zł, 4 zł, 5 zł. Do miasteczka tego przybyła z wycieczką klasa, dla której zakupiono bilety tak, aby każdy uczeń mógł pojechać na każdej karuzeli dokładnie raz. Wszystkie bilety kosztowały 280 zł. Ile biletów zakupiono?

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Suma trzech liczb jest równa 42. Znajdź te liczby, jeśli wiadomo, że pierwsza jest dwa razy mniejsza od drugiej, a druga stanowi połowę trzeciej.
 

Zwycięzca konkursu: Amelia Wójtowicz
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Zwycięzca konkursu: Katarzyna Charko
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Uwaga!: nagrodę-niespodziankę miesiąca lipca
wylosowała: Katarzyna Charko
uczennica: klasy trzeciej "c"
ze Szkoły Podstawowej nr 29 im. Adama Mickiewicza w Lublinie

  Nasza klasa liczy 28 uczniów. Liczba dziewcząt jest trzykrotnie większa od liczby chłopców. Ile dziewcząt jest w naszej klasie?

Zwycięzca konkursu: Amelia Wójtowicz
uczennica: klasy trzeciej "b"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Liczba 12 stanowi połowę połowy liczby (może zamiast liczby ilości) znaczków Tomka. Oblicz, ile znaczków ma Maciek, jeśli ma ich o połowę mniej niż Tomek.

Zwycięzca konkursu: brak nadesłanych rozwiązań

  Stół ma kształt prostokąta o obwodzie 480 cm. Szerokość stołu jest 8 razy krótsza od jego obwodu. Oblicz długość i szerokość tego stołu.

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Tomek i Maciek zbierają znaczki, liczba 12 to połowa połowy zbioru znaczków Tomka. Ile znaczków mają chłopcy razem, jeśli wiadomo, że Maciek ma o połowę znaczków mniej niż Tomek.

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

  Samochód osobowy „Fiat Seicento” spala 6 litrów benzyny na 100 km. Kierowca miał w zapasie 30 litrów benzyny. Dotychczas przebył trasę długości 350 km. Na przejechanie jeszcze ilu kilometrów starczy mu benzyny?

Zwycięzca konkursu: Natalia Kusiak
uczennica: klasy trzeciej "a"
z Zespołu Szkół nr 8, Szkoły Podstawowej nr 39 im. Aleksandra Kamińskiego w Lublinie

Gratulujemy Zwycięzcom
i zapraszamy
do udziału w konkursie "Zadań tygodnia"
w Nowym Roku Szkolnym 2016/2017.

                                                     Powrót na stronę główną